Bombe
ドイツの Enigma(エニグマ)暗号機を破るために英国で開発された電気・機械式の計算機である.まだ「電子式」ではないのでこれは最初のコンピュータではない.
Bombe を制作した場所はブレッチリーパーク(現在は公園)でいわばスパイ組織の黎明の場である.そこでは 007 シリーズの作者であるイアン・フレミングも活動していた
Enigma は複数の円盤の組み合わせで複雑な動作をする電気機械式の換字暗号機で解読不可能と言われていた.Enigma の円盤の数は3〜4枚で,バージョンによって異なる.Enigma を鹵獲(ろかく)した英国は円盤の動作をシミュレートするマシーン,Bombe を構築して解読を試みた.その努力は報われ,Bombe は Enigma を効率よく破った.
Bombe の開発に貢献したのはコンピュータ理論の父,アラン・チューリングである.

第二次大戦中は日独伊3国連合を組んでいたため,日本はドイツから Enigma を購入して円盤を5枚に増やしたものを「紫」暗号として使用していた.Bombe が Enigma を破り,その情報が米国に伝えられたため紫暗号も破られていたと言われる.
下図は再建されたBombeで,映画に使われたものである.これは単に外観だけでなく実際に動作するとのことである.画面に見える丸いものは多数のローターで,これらを回転させてEnigmaのキーに当る組み合わせを見つけようとするものである.可能な組み合わせは無数に考えられるので,異なった組み合わせに対して平行処理を行うことによって解読の効率を上げている.
Bombe(再建されたもの)

各種Enigma(現存する実物)
|
3枚ローター
|
3枚ローター
|
4枚ローター
|
 |
 |
 |
Enigma の円盤はそれぞれが文字を入れ替えるための接点を持っており,入れ替え方が円盤によって異なっている.また,円盤の回転角度によっても異なる.タイプライタのキーを1文字打つ毎に端の円盤が1文字分回転をする.その円盤が1回転すると隣の円盤が1文字分回転するようになっている.その結果「A」を繰り返し打っても訳の分からない文字列が発生することになる.このような構造であるから,Enigma 暗号を解読するためには,「どの円盤をどの組み合わせで使っているか」「それぞれの円盤の最初の角度は何か」が分からなければならない.
Enigma の優れている点は,暗号を発生できるだけでなく,受取った暗号文をタイプすると平文に翻訳(復号,デコード)できることである.小型で持ち運びに便利で,素早く暗号の生成と翻訳ができて解読不可能という先端技術の産物である.
しかし,Bombe はこれを破ったのである.余談であるが,第二次大戦中の日本の暗号は紫暗号だけでなく,戦闘単位間ではより簡単な暗号も使われていた.一般的には高度な紫暗号の方が破りにくいのであるが Enigma が破られていたために米国は紫暗号を解いていた.実は米国が破れなかった(破る努力をしなかった)のは「より簡単な」暗号の方だった.
Colossus(コロサス)
ドイツの暗号テレタイプ Lorenz(ロレンツ)を破るために英国で1943年に開発された世界で最初のコンピュータである.イギリス政府により1970年まで秘密のベールに閉ざされていたために後で示す ENIAC が最初のコンピュータと誤って伝えられた.また,各種資料も1960年に廃棄命令が出ていた.
Colossusは真空管時代のコンピュータであるが,既に現在のスーパーコンピュータと同様に「並列演算」を導入していた.そのため,半導体より遅い真空管でありながらエニグマを破るという目的には現時点でも十分と言える高速処理を行った.プログラムはメモリーに蓄える方法ではなく,パッチボードによる配線とスイッチの切換えによっていた.
現在の情報通信では「コンピュータ抜きでは何もできない」と言える.また,暗号は安全な通信を実現するために必須である.身近な例としては Web ページのアドレスの先頭にある「https:」がある.この「s」は secure を意味し,ページとの送受信が暗号化されていることを表している.最初のコンピュータであるコロサスが「情報」分野に使われたのは正に象徴的である.

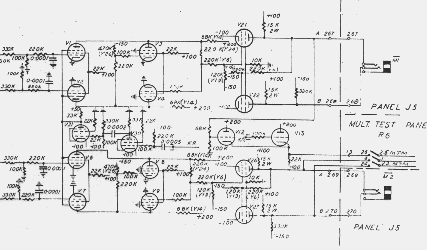
Colosussのシフトレジスタ回路図
技術者が隠匿していたもの
復元されたColossus(1996年)

Colossus は ブレッチリーパークで Tony Sale 達によって復元された.1960年に Colossus 関連の全ての文書の破棄が通達されたが,若干の技術者が隠し持っていたものをもとにして1996年に概ね復元された.もちろん使用している真空管は数十年昔のものである.1943年のモノクロ写真とほぼ同じ角度で撮影されているので,外観も忠実に復元しているのがよくわかる.
暗号テレタイプ(Lorentz)

Lorentz は Enigma 暗号機と異なり,より現代的な方法で暗号化を行った.そのため Bombe では対応できないものであった.Lorentz の暗号化は平文の文字列(1文字は5ビット)と「ランダムな文字列(0から31までの5ビットの乱数)」をビット対応の排他的論理和(XOR)の演算を行うことによっている.1文字を5ビットで表しているのでアルファベット26文字の他に記号が使える.そのためアルファベットだけの Enigma より読みやすい文章を作ることができた.
暗号の復号は暗号化に使ったのと同じランダム文字列と暗号の排他的論理和を求めることで行える.Lorentz も Enigma のように暗号作成と翻訳が同じ手順で行えることになる.しかも,長文の暗号を自動で作ることができ,通信(有線・無線)もモールス信号ではなく高速で行えるので Enigma より高度な装置である.
Lorentz では「ランダムな文字列」が重要な役割を果たしている.これは送り手と受け手で同じものでなければならない.本当のランダム文字列は送り手と受け手の両方で同じものを生成することは原理的に不可能なので「疑似乱数」を使用していた.疑似乱数は生成方式が同じなら,生成のための初期値(キー)を示すだけで送受の両者で同じ「ランダム」文字列を作ることができる.つまり暗号通信が成立するのである.
簡単な疑似乱数の生成法として,二乗最中法をあげることができる.これは 4桁の数字 X1(これがキーになる)を二乗した X12 の中 4桁を次の数 X2 とするものである.例えば,X1を 1234 とすると X2 は 1522756 であるので,X2 は 5227 になる.これを繰り返して,X3 = 3215, X4 = 3622,... と求める.この場合は 0 から 32 より大きな「乱数」となるが,それぞれを 32 で割った余りを使えば良いことになる(Xn mod 32).これにより,18, 11, 15, 6 .... が得られる.ただし,二乗最中法で得られるものは「乱数」としての品質が低く,かつ,Xn が 0 になるとその後はゼロが続くという大きな欠点を持っている.
Lorentz が破られた原因は通信文の再送信を同一キーで暗号化したことによる.もちろんドイツ軍は同一キーの使用を禁止していたが,現場の「ちょっとした」不手際が重大な結果を招く見本であった.
Colossus の復元写真に見られる滑車と紐のようなものは Lorents テレタイプの穿孔テープをループにつないで光学的に読み取るためのものである.左側の滑車の間が明るいのはそこに読み取り装置が在るからである.また,テーブルの上に載っているタイプライタは解読した暗号を印字するためのものである.
2番目のコンピュータ
Eniac(エニアック)
米国で1945年に着手された弾道計算用のコンピュータである.いわゆる「科学技術計算」用である.1970年まで Colossus に関する情報が秘匿されていたため Eniac が「最初の計算機」と言われていた.これも結線とスイッチの切換えによってプログラムを行った.下図の右に2人の女性がプログラムをしている光景が写っている.
|
Eniac(1946年)
|
Eniac のプログラム
|
|
 |
 |